The bplsr package implements the Bayesian partial least
squares regression model. It is a Bayesian factor model which emulates
the partial least squares (PLS) method. See Urbas et al. (2024) for
details.
# install.packages("devtools")
devtools::install_github("SzymonUrbas/bplsr")The following example illustrates how to carry out multivariate regression using BPLS on mid-infrared spectral data of milk samples:
library(bplsr)
X = milk_MIR$xMIR
Y = milk_MIR$yTraits[, c('Casein_content','Fat_content')]
set.seed(1)
# fit model to 75% of data and predict on remaining 25%
idx = sample(seq(nrow(X)),floor(nrow(X)*0.75),replace = FALSE)
Xtrain = X[idx,];Ytrain = Y[idx,]
Xtest = X[-idx,];Ytest = Y[-idx,]
# fit the model (MCMC takes time)
bplsr_Fit = bplsr(Xtrain,Ytrain)
# generate predictions
bplsr_pred = bplsr.predict(model = bplsr_Fit, newdata = Xtest)
# point predictions
head(bplsr_pred$Ytest)
#> Casein_content Fat_content
#> 5 3.142232 3.908393
#> 6 2.557213 4.109032
#> 7 2.739213 4.959536
#> 8 2.949198 5.058209
#> 9 2.773001 4.276898
#> 10 2.703331 4.500888
# lower and upper limits of prediction interval
head(bplsr_pred$Ytest_PI)
#> , , 2.5%
#>
#> Casein_content Fat_content
#> [1,] 2.824016 3.156057
#> [2,] 2.242527 3.343650
#> [3,] 2.421603 4.202634
#> [4,] 2.634399 4.301017
#> [5,] 2.449790 3.513700
#> [6,] 2.380676 3.732963
#>
#> , , 97.5%
#>
#> Casein_content Fat_content
#> [1,] 3.468311 4.665851
#> [2,] 2.883415 4.877653
#> [3,] 3.064176 5.742868
#> [4,] 3.270263 5.837006
#> [5,] 3.093597 5.043436
#> [6,] 3.023982 5.269628
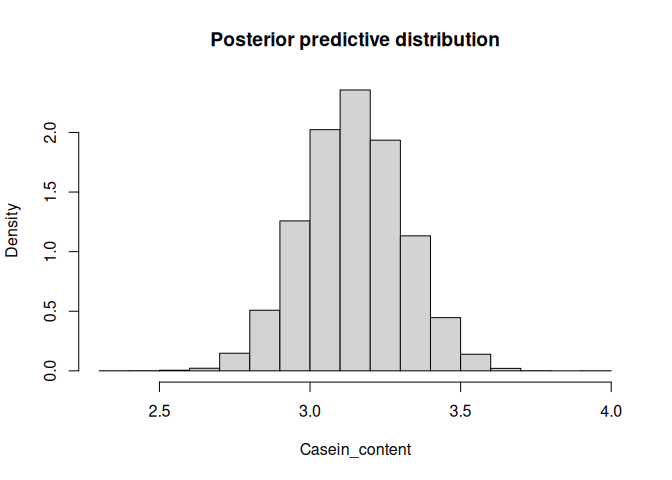
# plot of predictive posterior distribution for single test sample
hist(bplsr_pred$Ytest_dist[1,'Casein_content',], freq = F,
main = 'Posterior predictive distribution', xlab = 'Casein_content')
Urbas, S., Lovera, P., Daly, R., O’Riordan, A., Berry, D., and Gormley, I. C. (2024). “Predicting milk traits from spectral data using Bayesian probabilistic partial least squares regression.” The Annals of Applied Statistics, 18(4): 3486-3506 doi:10.1214/24-AOAS1947