
Implements conditional inference on normal variates as described in Lee, Sun, Sun and Taylor, “Exact Post Selection Inference, with Application to the Lasso.”
– Steven E. Pav, shabbychef@gmail.com
This package may be installed from CRAN; the latest version may be found on github via devtools, or installed via drat:
# CRAN
install.packages(c("epsiwal"))
# devtools
if (require(devtools)) {
# latest greatest
install_github("shabbychef/epsiwal")
}
# via drat:
if (require(drat)) {
drat:::add("shabbychef")
install.packages("epsiwal")
}First we perform some simulations under the null to show that the p-values are uniform. We draw a normal vector with identity covariance and zero mean, then flip the sign of each element to make them positive. We then perform inference on the sum of the mean values.
library(epsiwal)
p <- 20
mu <- rep(0, p)
Sigma <- diag(p)
A <- -diag(p)
b <- rep(0, p)
eta <- rep(1, p)
Sigma_eta <- diag(Sigma)
eta_mu <- as.numeric(t(eta) %*% mu)
set.seed(1234)
pvals <- replicate(1000, {
y <- rnorm(p, mean = mu, sd = sqrt(diag(Sigma)))
ay <- abs(y)
pconnorm(y = ay, A = A, b = b, eta = eta, Sigma_eta = Sigma_eta,
eta_mu = eta_mu)
})
qqplot(pvals, qunif(ppoints(length(pvals))), main = "p-values under procedure",
ylab = "theoretical", xlab = "empirical")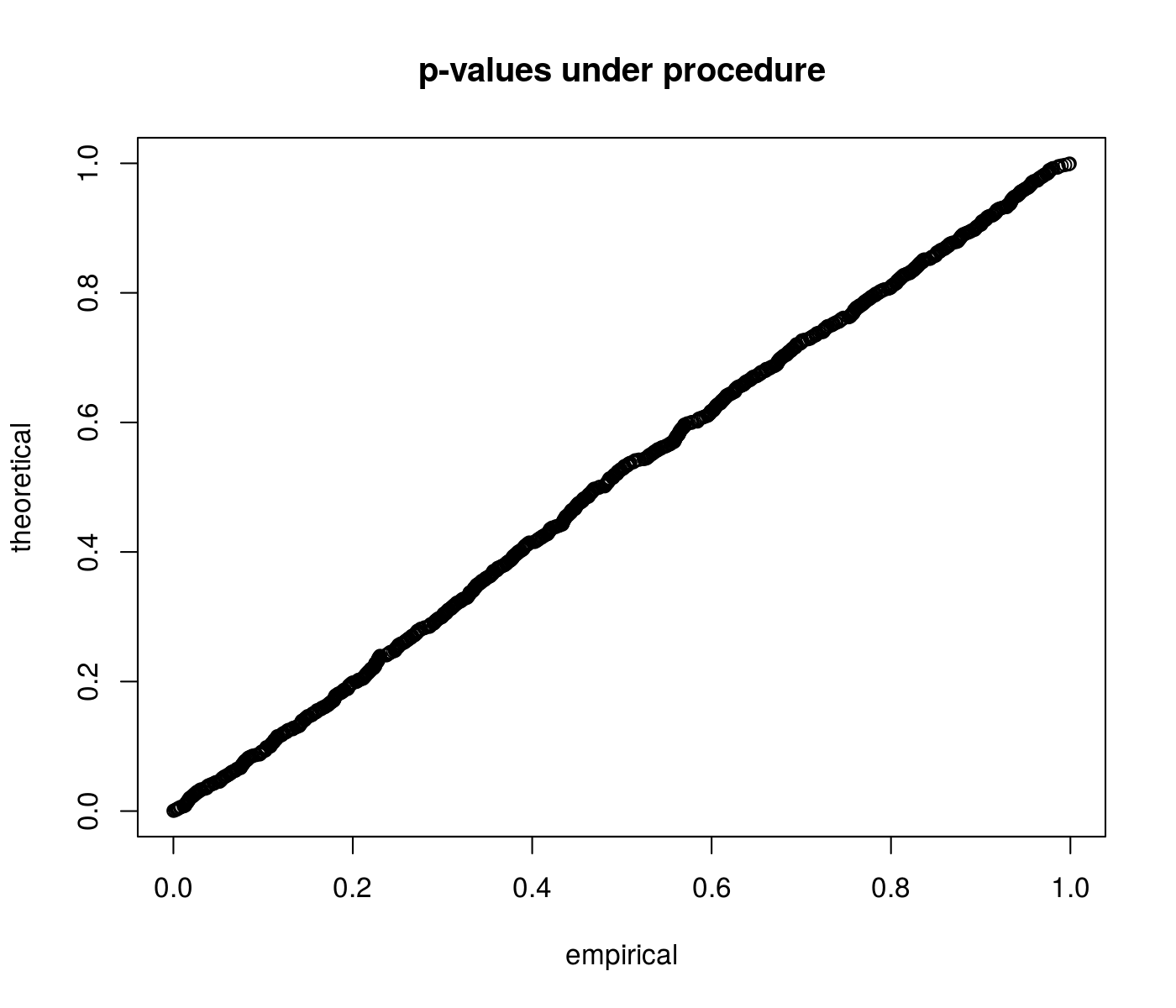
library(epsiwal)
p <- 20
mu <- rep(0, p)
Sigma <- diag(p)
A <- -diag(p)
b <- rep(0, p)
eta <- rep(1, p)
Sigma_eta <- diag(Sigma)
eta_mu <- as.numeric(t(eta) %*% mu)
type_I <- 0.05
set.seed(1234)
civals <- replicate(5000, {
y <- rnorm(p, mean = mu, sd = sqrt(diag(Sigma)))
ay <- abs(y)
ci <- ci_connorm(y = ay, A = A, b = b, p = type_I,
eta = eta, Sigma_eta = Sigma_eta)
})
cat("Empirical coverage of the", type_I, "confidence bound is around",
mean(civals < eta_mu), ".\n")## Empirical coverage of the 0.05 confidence bound is around 0.052 .PSAT
package, which supports similar procedures, but is not yet on
CRAN.SelectiveInference
package, which implements similar inferential procedures under
quadratic constraints, as detailed in Tibshirani, R. J., Taylor, J.,
Lockhart, R. and Tibshirani, R. Exact Post-Selection Inference
for Sequential Regression Procedures.