The fdacluster
package provides implementations of the \(k\)-means, hierarchical agglomerative and
DBSCAN clustering methods for functional data. Variability in functional
data is intrinsically divided into three components: amplitude,
phase and ancillary variability. The first two sources
of variability can be captured with a dedicated statistical analysis
that integrates a curve alignment step. The \(k\)-means and HAC algorithms implemented in
fdacluster
provide clustering structures that are based either on ampltitude
variation (default behavior) or phase variation. This is achieved by
jointly performing clustering and alignment of a functional data set.
The three main related functions are fdakmeans()
for the \(k\)-means, fdahclust()
for HAC and fdadbscan()
for DBSCAN. The methods handle multivariate
codomains.
You can install the official version from CRAN via:
install.packages("fdacluster")or you can opt to install the development version from GitHub with:
# install.packages("remotes")
remotes::install_github("astamm/fdacluster")Let us consider the following simulated example of \(30\) \(1\)-dimensional curves:
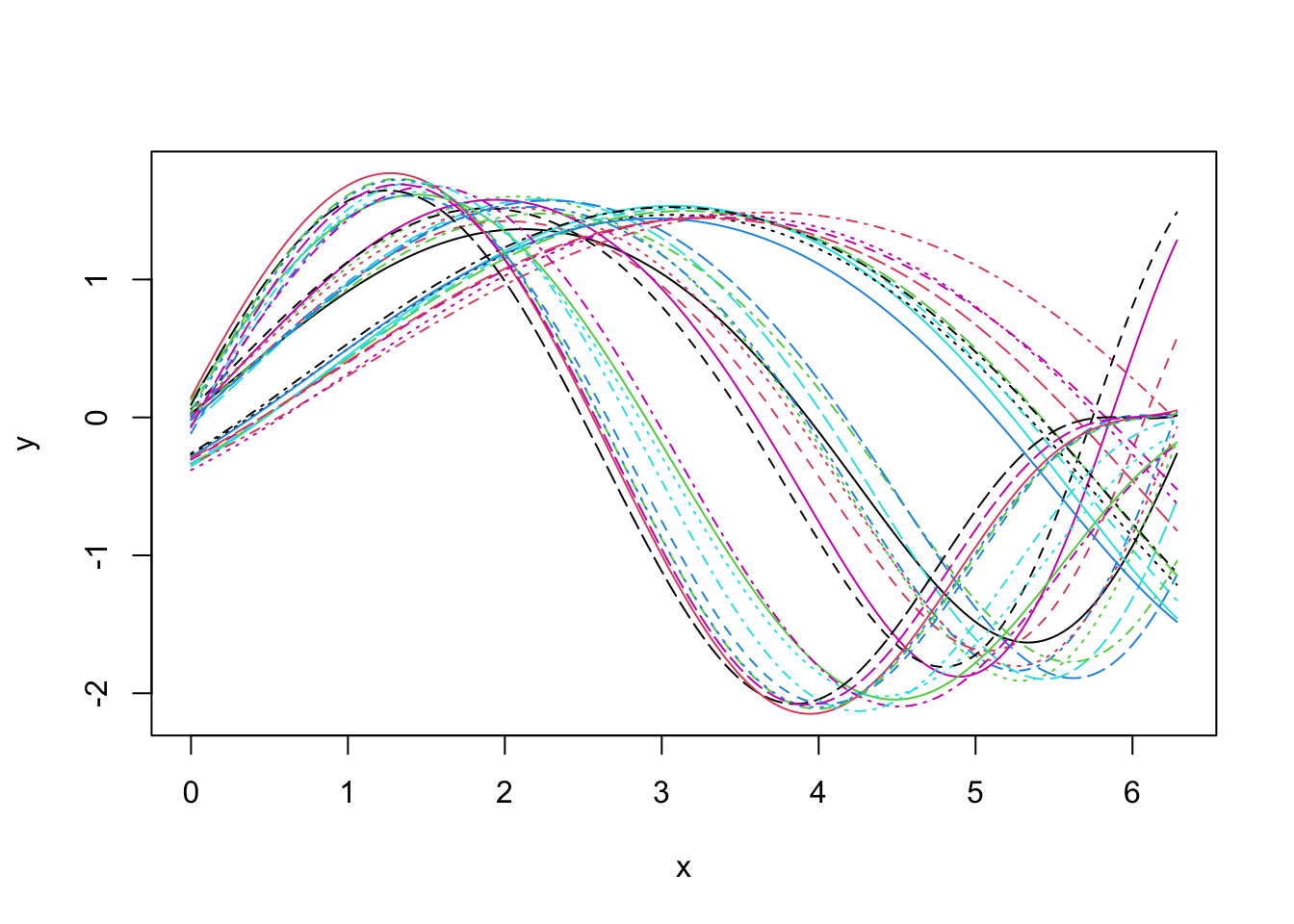
Looking at the data set, it seems that we shall expect \(3\) groups if we aim at clustering based on phase variability but probably only \(2\) groups if we search for a clustering structure based on amplitude variability.
We can perform \(k\)-means clustering based on amplitude variability as follows:
out1 <- fdakmeans(
simulated30$x,
simulated30$y,
seeds = c(1, 21),
n_clusters = 2,
centroid_type = "mean",
warping_class = "affine",
metric = "pearson",
cluster_on_phase = FALSE
)
#> Information about the data set:
#> - Number of observations: 30
#> - Number of dimensions: 1
#> - Number of points: 200
#>
#> Information about cluster initialization:
#> - Number of clusters: 2
#> - Initial seeds for cluster centers: 1 21
#>
#> Information about the methods used within the algorithm:
#> - Warping method: affine
#> - Center method: mean
#> - Dissimilarity method: pearson
#> - Optimization method: bobyqa
#>
#> Information about warping parameter bounds:
#> - Warping options: 0.1500 0.1500
#>
#> Information about convergence criteria:
#> - Maximum number of iterations: 100
#> - Distance relative tolerance: 0.001
#>
#> Information about parallelization setup:
#> - Number of threads: 1
#> - Parallel method: 0
#>
#> Other information:
#> - Use fence to robustify: 0
#> - Check total dissimilarity: 1
#> - Compute overall center: 0
#>
#> Running k-centroid algorithm:
#> - Iteration #1
#> * Size of cluster #0: 20
#> * Size of cluster #1: 10
#> - Iteration #2
#> * Size of cluster #0: 20
#> * Size of cluster #1: 10
#>
#> Active stopping criteria:
#> - Memberships did not change.All of fdakmeans(),
fdahclust()
and fdadbscan()
functions returns an object of class caps
(for Clustering with Amplitude and
Phase Separation) for which
S3 specialized methods of ggplot2::autoplot()
and graphics::plot()
have been implemented. Therefore, we can visualize the results simply
with:
plot(out1, type = "amplitude")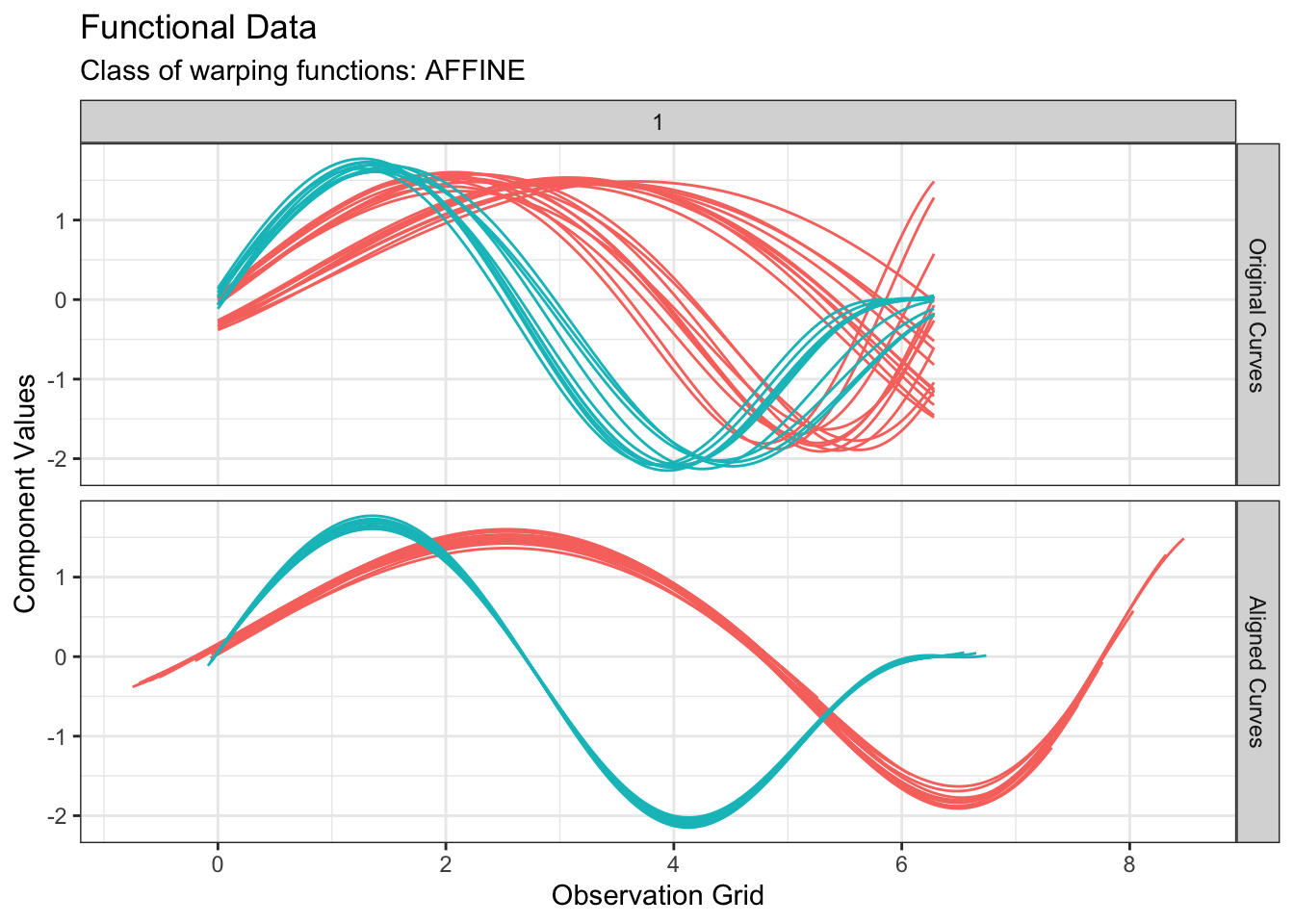
plot(out1, type = "phase")
We can perform \(k\)-means
clustering based on phase variability only by switch the
cluster_on_phase argument to TRUE:
out2 <- fdakmeans(
simulated30$x,
simulated30$y,
seeds = c(1, 11, 21),
n_clusters = 3,
centroid_type = "mean",
warping_class = "affine",
metric = "pearson",
cluster_on_phase = TRUE
)
#> Information about the data set:
#> - Number of observations: 30
#> - Number of dimensions: 1
#> - Number of points: 200
#>
#> Information about cluster initialization:
#> - Number of clusters: 3
#> - Initial seeds for cluster centers: 1 11 21
#>
#> Information about the methods used within the algorithm:
#> - Warping method: affine
#> - Center method: mean
#> - Dissimilarity method: pearson
#> - Optimization method: bobyqa
#>
#> Information about warping parameter bounds:
#> - Warping options: 0.1500 0.1500
#>
#> Information about convergence criteria:
#> - Maximum number of iterations: 100
#> - Distance relative tolerance: 0.001
#>
#> Information about parallelization setup:
#> - Number of threads: 1
#> - Parallel method: 0
#>
#> Other information:
#> - Use fence to robustify: 0
#> - Check total dissimilarity: 1
#> - Compute overall center: 0
#>
#> Running k-centroid algorithm:
#> - Iteration #1
#> * Size of cluster #0: 10
#> * Size of cluster #1: 10
#> * Size of cluster #2: 10
#> - Iteration #2
#> * Size of cluster #0: 10
#> * Size of cluster #1: 10
#> * Size of cluster #2: 10
#>
#> Active stopping criteria:
#> - Memberships did not change.We can inspect the result:
plot(out2, type = "amplitude")
plot(out2, type = "phase")
We can perform similar analyses using HAC or DBSCAN instead of \(k\)-means. The fdacluster
package also provides visualization tools to help choosing the optimal
number of cluster based on WSS and silhouette values. This can be
achieved by using a combination of the functions compare_caps()
and plot.mcaps().