iClusterVB allows for fast integrative clustering and feature selection for high dimensional data.
Using a variational Bayes approach, its key features - clustering of mixed-type data, automated determination of the number of clusters, and feature selection in high-dimensional settings - address the limitations of traditional clustering methods while offering an alternative and potentially faster approach than MCMC algorithms, making iClusterVB a valuable tool for contemporary data analysis challenges.
You can install iClusterVB from CRAN with:
install.packages("iClusterVB")You can install the development version of iClusterVB from GitHub with:
# install.packages("devtools")
devtools::install_github("AbdalkarimA/iClusterVB")Mandatory arguments
mydata: A list of length R, where R is the number of
datasets, containing the input data.
0’s must
be re-coded to another, non-0 value.dist: A vector of length R specifying the type of
data or distribution. Options include: “gaussian” (for continuous data),
“multinomial” (for binary or categorical data), and “poisson” (for count
data).
Optional arguments
K: The maximum number of clusters, with a default
value of 10. The algorithm will converge to a model with dominant
clusters, removing redundant clusters and automating the process of
determining the number of clusters.
initial_method: The method for the initial cluster
allocation, which the iClusterVB algorithm will then use to determine
the final cluster allocation. Options include “VarSelLCM” (default) for
VarSelLCM, “random” for a random sample, “kproto” for k-prototypes,
“kmeans” for k-means (continuous data only), “mclust” for mclust
(continuous data only), or “lca” for poLCA (categorical data
only).
VS_method: The feature selection method. The options
are 0 (default) for clustering without feature selection and 1 for
clustering with feature selection
initial_cluster: The initial cluster membership. The
default is NULL, which uses initial_method for initial
cluster allocation. If it is not NULL, it will overwrite the previous
initial values setting for this parameter.
initial_vs_prob: The initial feature selection
probability, a scalar. The default is NULL, which assigns a value of
0.5.
initial_fit: Initial values based on a previously
fitted iClusterVB model (an iClusterVB object). The default is
NULL.
initial_omega: Customized initial values for feature
inclusion probabilities. The default is NULL. If the argument is not
NULL, it will overwrite the previous initial values setting for this
parameter. If VS_method = 1, initial_omega is
a list of length R, and each element of the list is an array with
dim=c(N,p[[r]])). N is the sample size and p[[r]] is the number of
features for dataset r, r = 1,…,R.
initial_hyper_parameters: A list of the initial
hyper-parameters of the prior distributions for the model. The default
is NULL, which assigns alpha_00 = 0.001, mu_00 = 0,
s2_00 = 100, a_00 = 1, b_00 = 1, kappa_00 = 1, u_00 = 1, v_00 = 1.
These are \(\boldsymbol{\alpha}_0, \mu_0,
s^2_0, a_0, b_0, \boldsymbol{\kappa}_0, c_0, \text{and } d_0\)
described in https://dx.doi.org/10.2139/ssrn.4971680.
max_iter: The maximum number of iterations for the
VB algorithm. The default is 200.
early_stop: Whether to stop the algorithm upon
convergence or to continue until max_iter is reached.
Options are 1 (default) to stop when the algorithm converges, and 0 to
stop only when max_iter is reached.
per: Print information every “per” iteration. The
default is 10.
convergence_threshold: The convergence threshold for
the change in ELBO. The default is 0.0001.
We will demonstrate the clustering and feature selection performance
of iClusterVB using a simulated dataset comprising \(N = 240\) individuals and \(R = 4\) data views with different data
types. Two views were continuous,and one was count – a setup commonly
found in genomics data where gene or mRNA expression (continuous), and
DNA copy number (count) are observed. The true number of clusters (\(K\)) was set to 4, with balanced cluster
proportions (\(\pi_1 = 0.25, \pi_2 = 0.25,
\pi_3 = 0.25, \pi_4 = 0.25\)). Each data view consisted of \(p_r = 500\) features (\(r = 1, \dots, 3\)), totaling \(p = \sum_{r=1}^3 p_r = 1500\) features
across all views. Within each view, only 50 features (10%) were relevant
for clustering, while the remaining features were noise. The relevant
features were distributed across clusters as described in the table
below:
| Data View | Cluster | Distribution |
|---|---|---|
| 1 (Continuous) | Cluster 1 | \(\mathcal{N}(10, 1)\) (Relevant) |
| Cluster 2 | \(\mathcal{N}(5, 1)\) (Relevant) | |
| Cluster 3 | \(\mathcal{N}(-5, 1)\) (Relevant) | |
| Cluster 4 | \(\mathcal{N}(-10, 1)\) (Relevant) | |
| \(\mathcal{N}(0, 1)\) (Noise) | ||
| 2 (Continuous) | Cluster 1 | \(\mathcal{N}(-10, 1)\) (Relevant) |
| Cluster 2 | \(\mathcal{N}(-5, 1)\) (Relevant) | |
| Cluster 3 | \(\mathcal{N}(5, 1)\) (Relevant) | |
| Cluster 4 | \(\mathcal{N}(10, 1)\) (Relevant) | |
| \(\mathcal{N}(0, 1)\) (Noise) | ||
| 3 (Count) | Cluster 1 | \(\text{Poisson}(50)\) (Relevant) |
| Cluster 2 | \(\text{Poisson}(35)\) (Relevant) | |
| Cluster 3 | \(\text{Poisson}(20)\) (Relevant) | |
| Cluster 4 | \(\text{Poisson}(10)\) (Relevant) | |
| \(\text{Poisson}(2)\) (Noise) |
Distribution of relevant and noise features across clusters in each data view
The simulated dataset is included as a list in the package.
library(iClusterVB)
# Input data must be a list
dat1 <- list(gauss_1 = sim_data$continuous1_data,
gauss_2 = sim_data$continuous2_data,
multinomial_1 = sim_data$binary_data)
dist <- c("gaussian", "gaussian",
"multinomial")set.seed(123)
fit_iClusterVB <- iClusterVB(
mydata = dat1,
dist = dist,
K = 8,
initial_method = "VarSelLCM",
VS_method = 1, # Variable Selection is on
max_iter = 100,
per = 100
)
#> ------------------------------------------------------------
#> Pre-processing and initializing the model
#> ------------------------------------------------------------
#> ------------------------------------------------------------
#> Running the CAVI algorithm
#> ------------------------------------------------------------
#> iteration = 100 elbo = -21293757.232508table(fit_iClusterVB$cluster, sim_data$cluster_true)
#>
#> 1 2 3 4
#> 4 0 0 60 0
#> 5 0 60 0 0
#> 6 0 0 0 60
#> 8 60 0 0 0# We can obtain a summary using summary()
summary(fit_iClusterVB)
#> Total number of individuals:
#> [1] 240
#>
#> User-inputted maximum number of clusters: 8
#> Number of clusters determined by algorithm: 4
#>
#> Cluster Membership:
#> 4 5 6 8
#> 60 60 60 60
#>
#> # of variables above the posterior inclusion probability of 0.5 for View 1 - gaussian
#> [1] "54 out of a total of 500"
#>
#> # of variables above the posterior inclusion probability of 0.5 for View 2 - gaussian
#> [1] "59 out of a total of 500"
#>
#> # of variables above the posterior inclusion probability of 0.5 for View 3 - multinomial
#> [1] "500 out of a total of 500"plot(fit_iClusterVB)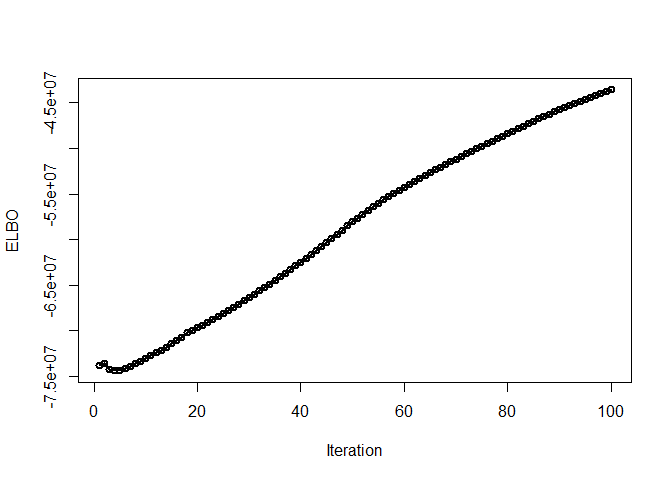

# The `piplot` function can be used to visualize the probability of inclusion
piplot(fit_iClusterVB)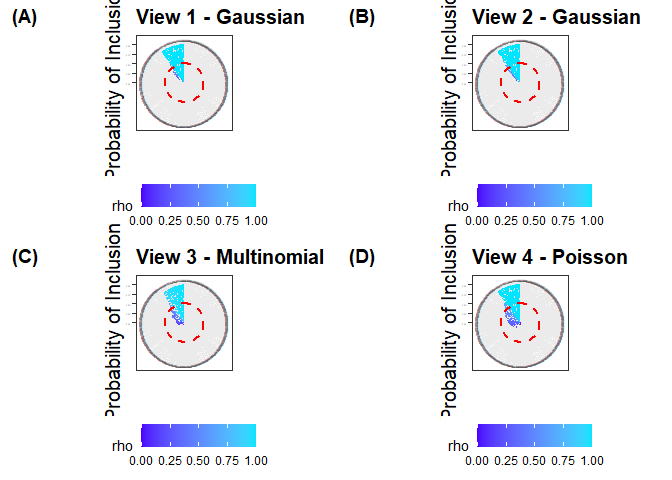
# The `chmap` function can be used to display heat maps for each data view
list_of_plots <- chmap(fit_iClusterVB, rho = 0,
cols = c("green", "blue",
"purple", "red"),
scale = "none")# The `grid.arrange` function from gridExtra can be used to display all the
# plots together
gridExtra::grid.arrange(grobs = list_of_plots, ncol = 2, nrow = 2)