The goal of igcop is to provide computational tools for the Integrated Gamma (IG) and Integrated Gamma Limit (IGL) copula families.
igcop is available on CRAN, and can be installed by running
The IG copula family is defined by parameters θ > 0 and α > 0, with the IGL copula family obtained with θ → ∞. See the vignette for a detailed definition.
Here are some contour plots of some normal scores copula densities.
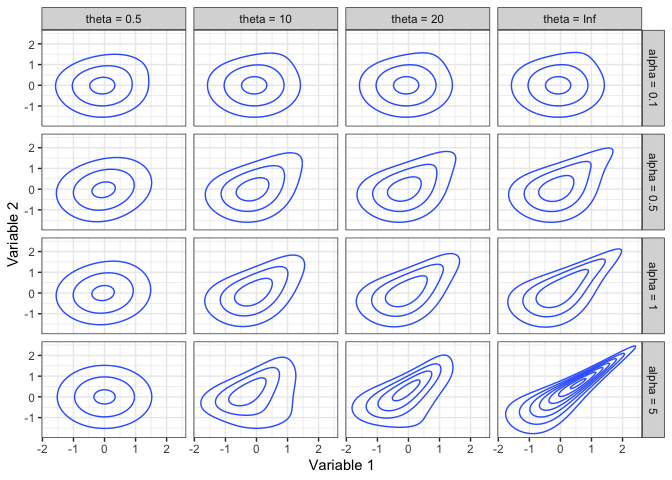
The IG and IGL copula families are unique in that, when used in a regression context, the conditional distribution of the response (the 2nd copula variable) has an Extreme Value Index that increases with the predictor for an IG copula, and reduces a heavy-tailed response to a light-tailed conditional distribution for an IGL copula. Specifically, the Extreme Value Index of the 2|1 distribution when Variable 2 has a Pareto(1) marginal distribution is 0 for an IGL copula, and is (1+θ(1−u))−1 for an IG copula (Coia 2017).
This package piggybacks on the base R syntax for distributions, such as dnorm() and pexp(), whose functions adopt the convention:
<prefix><name>For IG and IGL copulas:
<prefix> corresponds to one of:
p for cdf,d for density (and logd for log density),q for quantile (for conditional distributions only), andr for random number generation (not supported for conditional distributions).<name> corresponds to the possible names:
ig and igl correspond to an IG copula and IGL copula, respectively.condig12 and condigl12 correspond to a conditional distribution of the first variable given the second, of an IG copula and IGL copula respectively.condig21 and condigl21 correspond to a conditional distribution of the second variable given the first, of an IG copula and IGL copula respectively (also available as condig and condigl to match the syntax of the CopulaModel package).Here are some examples, starting with the density of an IG copula:
Computations are vectorized over each argument. Here’s the cdf and density of an IGL copula at different values:
u <- seq(0.1, 0.9, length.out = 9)
v <- seq(0.9, 0.5, length.out = 9)
pigl(u, v, alpha = 4)
#> [1] 0.1000000 0.2000000 0.2999711 0.3988536 0.4888134 0.5508382 0.5683229
#> [8] 0.5447653 0.4998090
digl(0.2, v, alpha = u)
#> [1] 0.8522462 0.8230206 0.8471676 0.8915708 0.9458967 1.0058156 1.0691273
#> [8] 1.1345476 1.2012456It doesn’t make sense to talk about quantiles for a multivariate distribution, so these are only defined for conditional distributions.
Here is an example of a distribution given the first variable (“2 given 1”). Note that the “2 given 1” distributions swap the u and v arguments to better align with the conditioning, and you can either explicitly include the 21 suffix or not.
qcondig(v, u, theta = 5, alpha = 3)
#> [1] 0.7435415 0.7228302 0.7121613 0.7073784 0.7056649 0.7039164 0.6972994
#> [8] 0.6777041 0.6356285
qcondig21(v, u, theta = 5, alpha = 3)
#> [1] 0.7435415 0.7228302 0.7121613 0.7073784 0.7056649 0.7039164 0.6972994
#> [8] 0.6777041 0.6356285Here is the corresponding “1 given 2” distribution. Since this is less common in regression scenarios, you have to explicitly add the 12 prefix for “1 given 2.”
qcondig12(v, u, theta = 5, alpha = 3)
#> [1] 0.8896885 0.8114873 0.7297887 0.6598357 0.6097781 0.5811235 0.5749922
#> [8] 0.5976573 0.6689895Generating 5 values from an IG copula:
set.seed(42)
rig(5, theta = 5, alpha = 4)
#> # A tibble: 5 × 2
#> u v
#> <dbl> <dbl>
#> 1 0.915 0.598
#> 2 0.937 0.848
#> 3 0.286 0.134
#> 4 0.830 0.761
#> 5 0.642 0.770Besides the copula quantities described above, the generating functions (as outlined in the vignette) are included in this package as internal functions, and directly link to C++. The notation is:
igl_gen();igl_kappa();interp_gen(); andinterp_kappa().Related functions have the following suffixes:
_inv: function inverse._D: function derivative._D1: function derivative with respect to first argument.There are three functions involved when linking to C:
igl_gen()) recycles the arguments by passing them through the formals_to() function, which uses vctrs::vec_recycle_common()._vec suffix, which passes these functions into C++ (via the infrastructure created by running Rcpp::compileAttributes())._vec suffix. These functions loop along each entry, and feeds the scalar values into a C++ function for computation (either with the _single prefix, or the _algo prefix when the function contains a Newton-Raphson algorithm).Map of dependencies among functions:
igl_gen : pgammaigl_gen_D : pgammaigl_gen_inv_algo : qgamma igl_gen igl_gen_Digl_gen_inv : igl_gen_inv_algointerp_gen : igl_geninterp_gen_D1 : igl_geninterp_gen_inv_algo : igl_gen_inv_algo interp_gen interp_gen_D1interp_gen_inv : interp_gen_inv_algoigl_kappa : pgammaigl_kappa_D : dgammaigl_kappa_inv : qgammainterp_kappa : igl_kappainterp_kappa_D1 : igl_kappa igl_kappa_Dinterp_kappa_inv_algo : igl_kappa_inv interp_kappa igl_kappa igl_kappa_D interp_kappa_invinterp_kappa_inv : interp_kappa_inv_algopcondig21 : interp_gen_inv interp_kappaqcondig21 : interp_kappa_inv interp_genqcondig12_algo : interp_gen_inv igl_gen igl_gen_D pcondig12qcondig12 : qcondig12_algopcondig12 : interp_gen_inv interp_gen_D1dig : interp_gen_inv interp_kappa_D1 interp_gen_D1logdig : interp_gen_inv igl_kappa igl_kappa_D igl_gen igl_gen_Dpig : interp_gen_invrig : qcondig21qcondigl21 : igl_kappa_invpcondigl21 : igl_gen_inv igl_kappapcondigl12 : igl_gen_inv igl_gen_Dqcondigl12 : igl_gen_inv pgamma qgammadigl : igl_gen_inv igl_kappa_D igl_gen_Dpigl : igl_gen_inv igl_genrigl : qcondigl21Package developed and maintained by Vincenzo Coia, with thanks to Harry Joe for his help converting the Newton Raphson algorithms and related functions to C (originally coded in R in igcop Version 0.2.0).
Coia, Vincenzo. 2017. “Forecasting of Nonlinear Extreme Quantiles Using Copula Models.” PhD Dissertation; The University of British Columbia.