README

Furthermore, the function additive_shap() produces SHAP values for additive models fitted via lm(), glm(), mgcv::gam(), mgcv::bam(), gam::gam(), survival::coxph(), or survival::survreg(). It is exponentially faster than permshap() and kernelshap(), with identical results when the background dataset of the latter equals the full training data.

Kernel SHAP or permutation SHAP?

Kernel SHAP has been introduced in [2] as an approximation of permutation SHAP [1]. For up to ten features, exact calculations are realistic for both algorithms. Since exact Kernel SHAP is still only an approximation of exact permutation SHAP, the latter should be preferred in this case, even if the results are often very similar.

A situation where the two approaches give different results: The model has interactions of order three or higher.

Typical workflow to explain any model

Installation

# From CRAN
install.packages("kernelshap")

# Or the development version:
devtools::install_github("ModelOriented/kernelshap")

Basic Usage

Let’s model diamond prices with a random forest. As an alternative, you could use the {treeshap} package in this situation.

library(kernelshap)
library(ggplot2)
library(ranger)
library(shapviz)

diamonds <- transform(
  diamonds,
  log_price = log(price), 
  log_carat = log(carat)
)

xvars <- c("log_carat", "clarity", "color", "cut")

fit <- ranger(
  log_price ~ log_carat + clarity + color + cut, 
  data = diamonds, 
  num.trees = 100,
  seed = 20
)
fit  # OOB R-squared 0.989

# 1) Sample rows to be explained
set.seed(10)
X <- diamonds[sample(nrow(diamonds), 1000), xvars]

# 2) Optional: Select background data. If not specified, a random sample of 200 rows
#    from X is used
bg_X <- diamonds[sample(nrow(diamonds), 200), ]

# 3) Crunch SHAP values for all 1000 rows of X (54 seconds)
# Note: Since the number of features is small, we use permshap()
system.time(
  ps <- permshap(fit, X, bg_X = bg_X)
)
ps

# SHAP values of first observations:
      log_carat     clarity       color         cut
[1,]  1.1913247  0.09005467 -0.13430720 0.000682593
[2,] -0.4931989 -0.11724773  0.09868921 0.028563613

# Kernel SHAP gives almost the same:
system.time(  # 49 s
  ks <- kernelshap(fit, X, bg_X = bg_X)
)
ks
#       log_carat     clarity       color        cut
# [1,]  1.1911791  0.0900462 -0.13531648 0.001845958
# [2,] -0.4927482 -0.1168517  0.09815062 0.028255442

# 4) Analyze with our sister package {shapviz}
ps <- shapviz(ps)
sv_importance(ps)
sv_dependence(ps, xvars)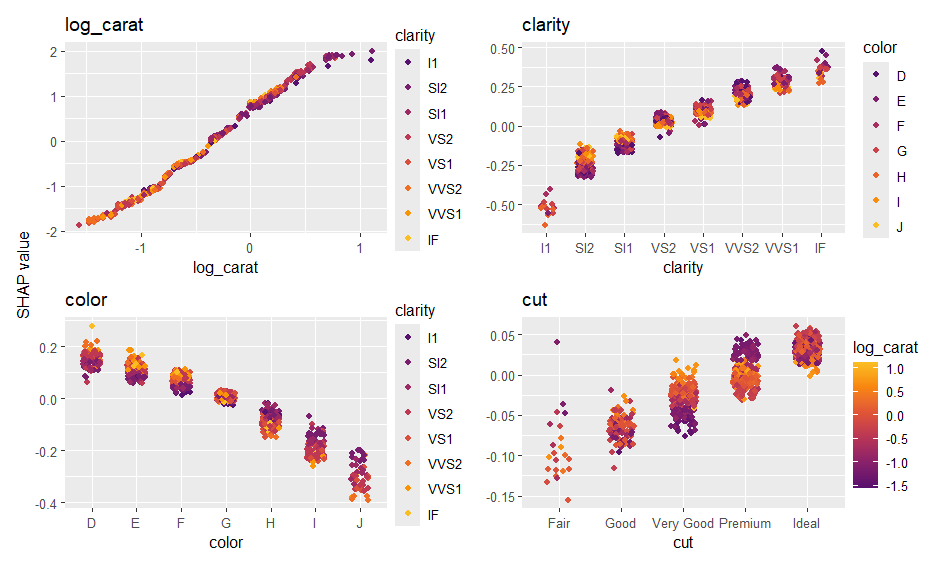

More Examples

{kernelshap} can deal with almost any situation. We will show some of the flexibility here. The first two examples require you to run at least up to Step 2 of the “Basic Usage” code.

Parallel computing

Parallel computing is supported via {foreach}. Note that this does not work with all models, and that there is no progress bar.

On Windows, sometimes not all packages or global objects are passed to the parallel sessions. Often, this can be fixed via parallel_args, see the generalized additive model below.

library(doFuture)
library(mgcv)

registerDoFuture()
plan(multisession, workers = 4)  # Windows
# plan(multicore, workers = 4)   # Linux, macOS, Solaris

fit <- gam(log_price ~ s(log_carat) + clarity * color + cut, data = diamonds)

system.time(  # 9 seconds in parallel
  ps <- permshap(fit, X, parallel = TRUE, parallel_args = list(.packages = "mgcv"))
)
ps

# SHAP values of first observations:
#      log_carat    clarity       color         cut
# [1,]   1.26801  0.1023518 -0.09223291 0.004512402
# [2,]  -0.51546 -0.1174766  0.11122775 0.030243973

# Because there are no interactions of order above 2, Kernel SHAP gives the same:
system.time(  # 27 s non-parallel
  ks <- kernelshap(fit, X, bg_X = bg_X)
)
all.equal(ps$S, ks$S)
# [1] TRUE

# Now the usual plots:
sv <- shapviz(ps)
sv_importance(sv, kind = "bee")
sv_dependence(sv, xvars)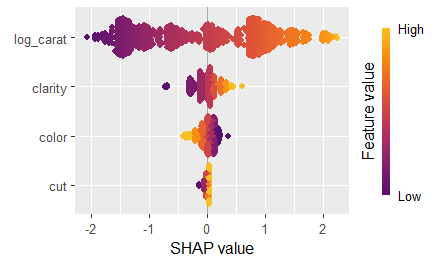

Taylored predict()

In this {keras} example, we show how to use a tailored predict() function that complies with

library(keras)

nn <- keras_model_sequential()
nn |>
  layer_dense(units = 30, activation = "relu", input_shape = 4) |>
  layer_dense(units = 15, activation = "relu") |>
  layer_dense(units = 1)

nn |>
  compile(optimizer = optimizer_adam(0.001), loss = "mse")

cb <- list(
  callback_early_stopping(patience = 20),
  callback_reduce_lr_on_plateau(patience = 5)
)
       
nn |>
  fit(
    x = data.matrix(diamonds[xvars]),
    y = diamonds$log_price,
    epochs = 100,
    batch_size = 400, 
    validation_split = 0.2,
    callbacks = cb
  )

pred_fun <- function(mod, X) 
  predict(mod, data.matrix(X), batch_size = 1e4, verbose = FALSE)

system.time(  # 60 s
  ps <- permshap(nn, X, bg_X = bg_X, pred_fun = pred_fun)
)

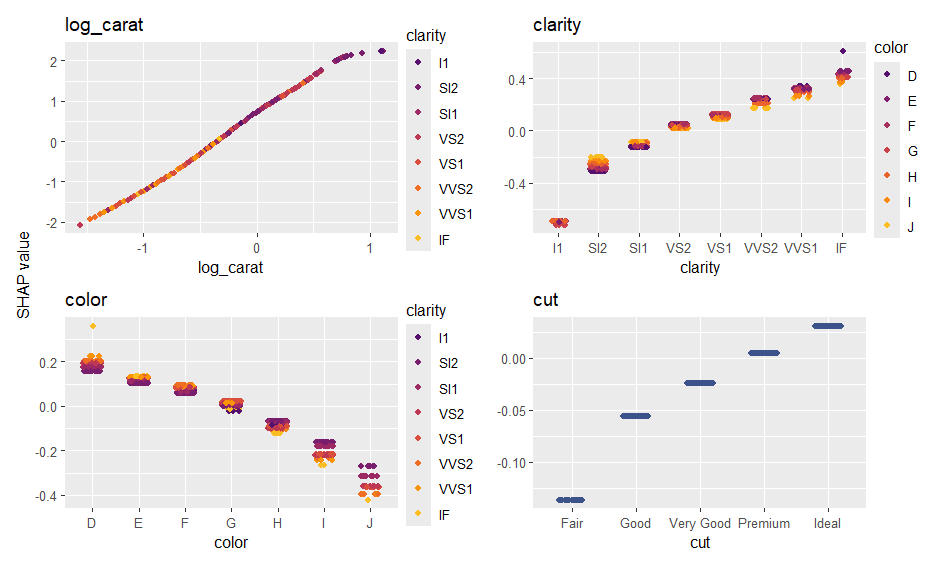
ps <- shapviz(ps)
sv_importance(ps, show_numbers = TRUE)
sv_dependence(ps, xvars)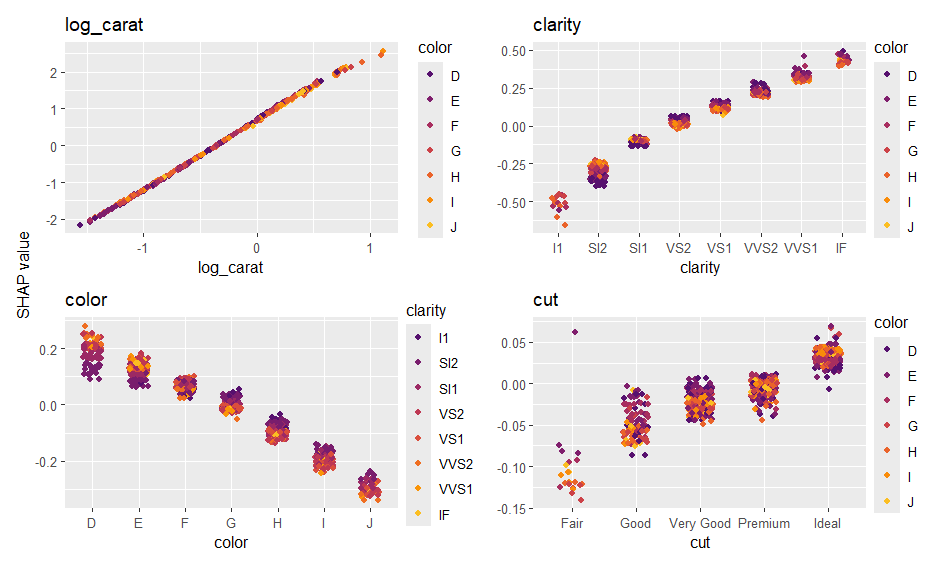

Additive SHAP

The additive explainer extracts the additive contribution of each feature from a model of suitable class.

fit <- lm(log(price) ~ log(carat) + color + clarity + cut, data = diamonds)
shap_values <- additive_shap(fit, diamonds) |> 
  shapviz()
sv_importance(shap_values)
sv_dependence(shap_values, v = "carat", color_var = NULL)

Multi-output models

library(kernelshap)
library(ranger)
library(shapviz)

set.seed(1)

# Probabilistic classification
fit_prob <- ranger(Species ~ ., data = iris, probability = TRUE)
ps_prob <- permshap(fit_prob, X = iris[-5]) |> 
  shapviz()
sv_importance(ps_prob)
sv_dependence(ps_prob, "Petal.Length")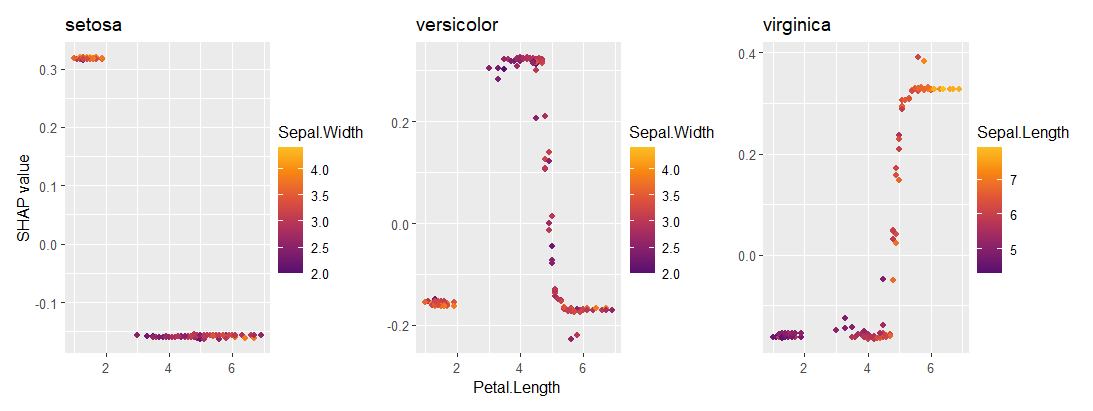

Meta-learners

Meta-learning packages like {tidymodels}, {caret} or {mlr3} are straightforward to use. The following examples additionally shows that the ... arguments of permshap() and kernelshap() are passed to predict().

Tidymodels

library(kernelshap)
library(tidymodels)

set.seed(1)

iris_recipe <- iris |> 
  recipe(Species ~ .)

mod <- rand_forest(trees = 100) |>
  set_engine("ranger") |> 
  set_mode("classification")
  
iris_wf <- workflow() |>
  add_recipe(iris_recipe) |>
  add_model(mod)

fit <- iris_wf |>
  fit(iris)

system.time(  # 4s
  ps <- permshap(fit, iris[-5], type = "prob")
)
ps

# Some values
$.pred_setosa
     Sepal.Length Sepal.Width Petal.Length Petal.Width
[1,]   0.02186111 0.012137778    0.3658278   0.2667667
[2,]   0.02628333 0.001315556    0.3683833   0.2706111

caret

library(kernelshap)
library(caret)

fit <- train(
  Sepal.Length ~ ., 
  data = iris, 
  method = "lm", 
  tuneGrid = data.frame(intercept = TRUE),
  trControl = trainControl(method = "none")
)

ps <- permshap(fit, iris[-1])

mlr3

library(kernelshap)
library(mlr3)
library(mlr3learners)

set.seed(1)

task_classif <- TaskClassif$new(id = "1", backend = iris, target = "Species")
learner_classif <- lrn("classif.rpart", predict_type = "prob")
learner_classif$train(task_classif)

x <- learner_classif$selected_features()

# Don't forget to pass predict_type = "prob" to mlr3's predict()
ps <- permshap(
  learner_classif, X = iris, feature_names = x, predict_type = "prob"
)
ps
# $setosa
#      Petal.Length Petal.Width
# [1,]    0.6666667           0
# [2,]    0.6666667           0

References

[1] Erik Štrumbelj and Igor Kononenko. Explaining prediction models and individual predictions with feature contributions. Knowledge and Information Systems 41, 2014.

[2] Scott M. Lundberg and Su-In Lee. A Unified Approach to Interpreting Model Predictions. Advances in Neural Information Processing Systems 30, 2017.

[3] Ian Covert and Su-In Lee. Improving KernelSHAP: Practical Shapley Value Estimation Using Linear Regression. Proceedings of The 24th International Conference on Artificial Intelligence and Statistics, PMLR 130:3457-3465, 2021.

kernelshap

Overview