

paleopop is part of the poemsverse. poems
is a spatially-explicit, process-explicit, pattern-oriented framework
for modeling population dynamics. This extension adds functionality for
modeling large populations at generational time-steps over
paleontological time-scales.
You can install the latest release of paleopop from CRAN
with:
install.packages("paleopop")
#> Installing package into '/home/runner/work/_temp/Library'
#> (as 'lib' is unspecified)You can install the development version from GitHub with:
# install.packages("devtools")
devtools::install_github("GlobalEcologyLab/paleopop")poems and paleopop are based on R6 class objects. R is primarily a
functional programming language; if you want to simulate a
population, you might use the lapply or
replicate functions to repeat a generative function like
rnorm. R6 creates an object-oriented programming
language inside of R, so instead of using functions on other functions,
in these packages we simulate populations using methods attached to
objects. Think of R6 objects like machines, and methods like switches
you can flip on the machines.
One of the major additions in paleopop is the
PaleoRegion R6 class, which allows for regions that change
over time due to ice sheets, sea level, bathymetry, and so on. The plots
below show the temporal mask functionality of the
PaleoRegion object. The temporal mask indicates cells that
are occupiable at each time step with a 1 and unoccupiable cells with a
NA. In this example, I use the
temporal_mask_raster method to show how “Ring Island”
changes at time step 10 due to a drop in sea level.
library(poems)
library(paleopop)
coordinates <- data.frame(x = rep(seq(-178.02, -178.06, -0.01), 5),
y = rep(seq(19.02, 19.06, 0.01), each = 5),
z = rep(1, 25))
template_raster <- raster::rasterFromXYZ(coordinates,
crs = "+proj=longlat +datum=WGS84 +ellps=WGS84 +towgs84=0,0,0")
sealevel_raster <- template_raster
template_raster[][c(7:9, 12:14, 17:19)] <- NA # make Ring Island
sealevel_raster[][c(7:9, 12:14, 17:18)] <- NA
raster_stack <- raster::stack(x = append(replicate(9, template_raster), sealevel_raster))
region <- PaleoRegion$new(template_raster = raster_stack)
raster::plot(region$temporal_mask_raster()[[1]], main = "Ring Island (first timestep)",
xlab = "Longitude (degrees)", ylab = "Latitude (degrees)",
colNA = "blue")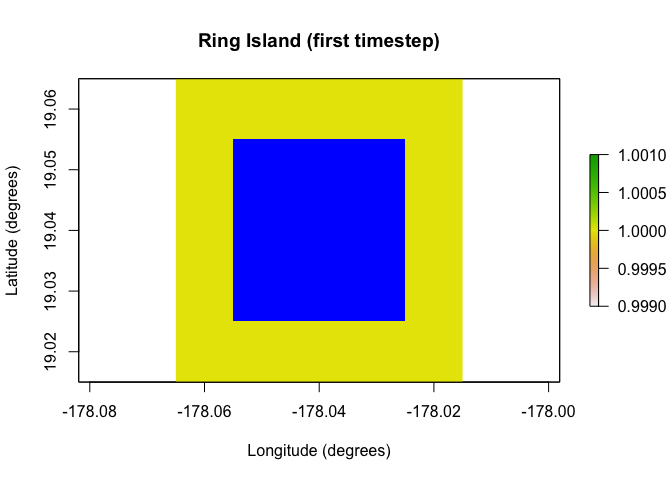
raster::plot(region$temporal_mask_raster()[[10]], main = "Ring Island (last timestep)",
xlab = "Longitude (degrees)", ylab = "Latitude (degrees)",
colNA = "blue")
paleopop also includes the PaleoPopModel
class, which sets up the population model structure. Here I show a very
minimalist setup of a model template using this class.
model_template <- PaleoPopModel$new(
region = region, # makes the simulation spatially explicit
time_steps = 10, # number of time steps to simulate
years_per_step = 12, # years per generational time-step
standard_deviation = 0.1, # SD of growth rate
growth_rate_max = 0.6, # maximum growth rate
harvest = F, # are the populations harvested?
populations = 17, # total occupiable cells over time
initial_abundance = seq(9000, 0, -1000), # initial pop. sizes
transition_rate = 1.0, # transition rate between generations
carrying_capacity = rep(1000, 17), # static carrying capacity
dispersal = (!diag(nrow = 17, ncol = 17))*0.05, # dispersal rates
density_dependence = "logistic", # type of density dependence
dispersal_target_k = 10, # minimum carrying capacity to attract dispersers
occupancy_threshold = 1, # lower than this # of pops. means extinction
abundance_threshold = 10, # threshold for Allee effect
results_selection = c("abundance") # what outputs do you want in results?
)The paleopop_simulator function accepts a PaleoPopModel
object or a named list as input to simulate populations over paleo time
scales, and the PaleoPopResults class stores the outputs
from the paleo population simulator.
results <- paleopop_simulator(model_template)
results # examine
#> $abundance
#> [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
#> [1,] 88 150 258 403 606 902 1049 962 1096 1400
#> [2,] 330 563 733 794 701 781 786 865 964 1104
#> [3,] 1199 1104 991 1087 1257 1062 998 1016 1025 1055
#> [4,] 306 465 655 681 954 959 955 934 1008 813
#> [5,] 101 150 248 369 488 674 826 973 1048 1038
#> [6,] 336 468 639 687 840 929 972 957 1028 991
#> [7,] 575 634 888 929 970 907 912 1022 1058 905
#> [8,] 1123 1086 1140 1215 1140 836 955 934 938 826
#> [9,] 961 834 908 947 1045 980 964 958 1070 904
#> [10,] 0 0 0 0 0 0 0 0 0 0
#> [11,] 0 0 0 0 0 0 0 0 0 0
#> [12,] 0 0 0 0 0 0 0 0 0 0
#> [13,] 497 666 912 1033 997 972 1023 924 923 929
#> [14,] 64 92 180 258 450 552 761 1039 990 1067
#> [15,] 595 720 881 779 1016 984 933 973 1156 1091
#> [16,] 452 742 850 931 950 1050 1017 1093 1007 1046
#> [17,] 1182 1017 1151 1119 904 689 854 904 890 958
raster::plot(region$raster_from_values(results$abundance[,10]),
main = "Final abundance", xlab = "Longitude (degrees)",
ylab = "Latitude (degrees)", colNA = "blue")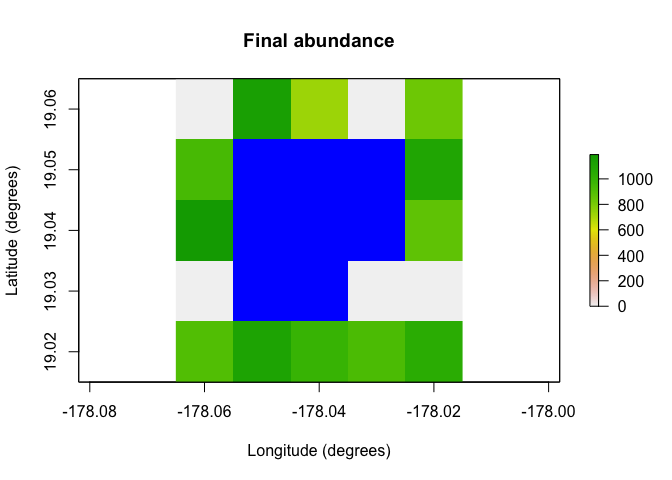
A practical example of how to use paleopop, with more
complex parameterization, can be found in the vignette.
You may cite paleopop in publications using our software
paper in Global Ecology and Biogeography:
Pilowsky, J. A., Haythorne, S., Brown, S. C., Krapp, M., Armstrong, E., Brook, B. W., Rahbek, C., & Fordham, D. A. (2022). Range and extinction dynamics of the steppe bison in Siberia: A pattern‐oriented modelling approach. Global Ecology and Biogeography, 31(12), 2483-2497.