R package pomdp - Infrastructure for Partially Observable Markov Decision Processes (POMDP) R package pomdp - Infrastructure for Partially Observable Markov Decision Processes (POMDP)
A partially observable Markov decision process (POMDP) models an agent decision process where the agent cannot directly observe the environment’s state, but has to rely on observations. The goal is to find an optimal policy to guide the agent’s actions.
The pomdp package provides the infrastructure to define and analyze the solutions of optimal control problems formulated as Partially Observable Markov Decision Processes (POMDP). The package uses the solvers from pomdp-solve (Cassandra, 2015) available in the companion R package pomdpSolve to solve POMDPs using a variety of exact and approximate algorithms.
The package provides fast functions (using C++, sparse matrix representation, and parallelization with foreach) to perform experiments (sample from the belief space, simulate trajectories, belief update, calculate the regret of a policy). The package also interfaces to the following algorithms:
If you are new to POMDPs then start with the POMDP Tutorial.
To cite package ‘pomdp’ in publications use:
Hahsler M (2023). pomdp: Infrastructure for Partially Observable Markov Decision Processes (POMDP). R package version 1.1.2, https://CRAN.R-project.org/package=pomdp.
@Manual{,
title = {pomdp: Infrastructure for Partially Observable Markov Decision
Processes (POMDP)},
author = {Michael Hahsler},
year = {2023},
note = {R package version 1.1.2},
url = {https://CRAN.R-project.org/package=pomdp},
}Stable CRAN version: Install from within R with
Current development version: Install from r-universe.
install.packages("pomdp",
repos = c("https://mhahsler.r-universe.dev". "https://cloud.r-project.org/"))Solving the simple infinite-horizon Tiger problem.
## POMDP, list - Tiger Problem
## Discount factor: 0.75
## Horizon: Inf epochs
## Size: 2 states / 3 actions / 2 obs.
## Normalized: FALSE
##
## Solved: FALSE
##
## List components: 'name', 'discount', 'horizon', 'states', 'actions',
## 'observations', 'transition_prob', 'observation_prob', 'reward',
## 'start', 'terminal_values'## POMDP, list - Tiger Problem
## Discount factor: 0.75
## Horizon: Inf epochs
## Size: 2 states / 3 actions / 2 obs.
## Normalized: FALSE
##
## Solved:
## Method: grid
## Solution converged: TRUE
## # of alpha vectors: 5
## Total expected reward: 1.933439
##
## List components: 'name', 'discount', 'horizon', 'states', 'actions',
## 'observations', 'transition_prob', 'observation_prob', 'reward',
## 'start', 'solution'Display the value function.
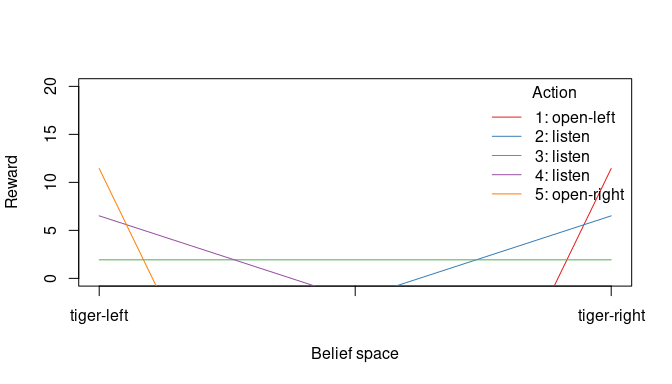
Display the policy graph.
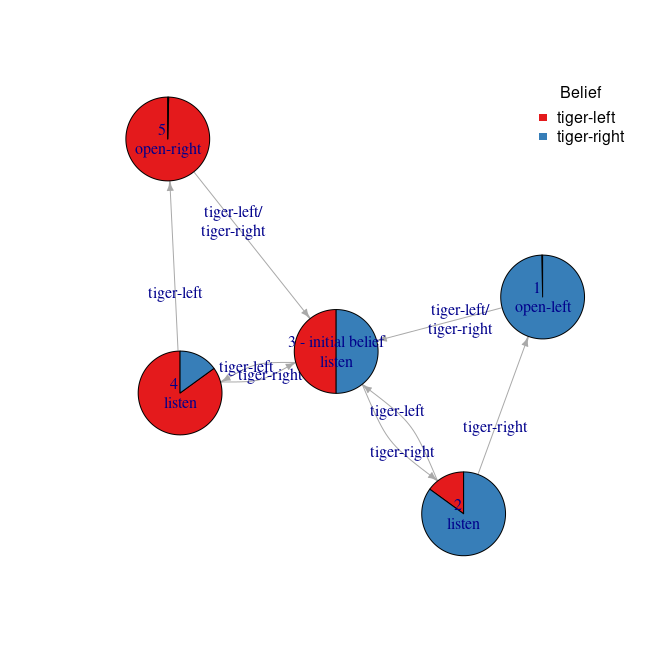
Development of this package was supported in part by National Institute of Standards and Technology (NIST) under grant number 60NANB17D180.
Cassandra, Anthony R. 2015. “The POMDP Page.” https://www.pomdp.org.
Cassandra, Anthony R., Michael L. Littman, and Nevin Lianwen Zhang. 1997. “Incremental Pruning: A Simple, Fast, Exact Method for Partially Observable Markov Decision Processes.” In UAI’97: Proceedings of the Thirteenth Conference on Uncertainty in Artificial Intelligence, 54–61.
Kurniawati, Hanna, David Hsu, and Wee Sun Lee. 2008. “SARSOP: Efficient Point-Based POMDP Planning by Approximating Optimally Reachable Belief Spaces.” In In Proc. Robotics: Science and Systems.
Littman, Michael L., Anthony R. Cassandra, and Leslie Pack Kaelbling. 1995. “Learning Policies for Partially Observable Environments: Scaling Up.” In Proceedings of the Twelfth International Conference on International Conference on Machine Learning, 362–70. ICML’95. San Francisco, CA, USA: Morgan Kaufmann Publishers Inc.
Monahan, G. E. 1982. “A Survey of Partially Observable Markov Decision Processes: Theory, Models, and Algorithms.” Management Science 28 (1): 1–16.
Pineau, Joelle, Geoff Gordon, and Sebastian Thrun. 2003. “Point-Based Value Iteration: An Anytime Algorithm for POMDPs.” In Proceedings of the 18th International Joint Conference on Artificial Intelligence, 1025–30. IJCAI’03. San Francisco, CA, USA: Morgan Kaufmann Publishers Inc.
Sondik, E. J. 1971. “The Optimal Control of Partially Observable Markov Decision Processes.” PhD thesis, Stanford, California.
Zhang, Nevin L., and Wenju Liu. 1996. “Planning in Stochastic Domains: Problem Characteristics and Approximation.” HKUST-CS96-31. Hong Kong University.